Respuesta de circuitos de 1r orden.
Circuitos de 1r orden:
Son circuitos con un elemento almacenador de energía o varios que puedan ser sustituidos por uno equivalente.
3.1 Respuesta natural de un circuito RL
Objetivo: Calcular la evolución de la corriente i(t) en el circuito RL cuando desconectamos la alimentación.
El interruptor ha permanecido mucho tiempo cerrado.
Para t menor que 0 toda la corriente circulaba por la bobina (L cortocircuitada) entonces iL(t=0-) = Ig (condición inicial).
Si abrimos el interruptor, el circuito quedará:
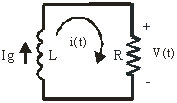
Aplicando KVL:
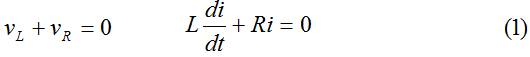
Solución general de este tipo de ecuaciones:
Cálculo de s:
descartando la solución trivial A=0
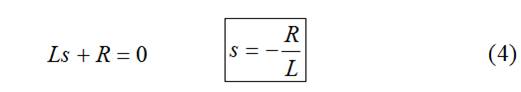
Cálculo de A:
y condiciones iniciales
Sustituyendo (5) y (4) en (2)
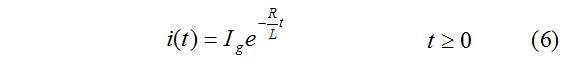
La i(t) se decrementa exponencialmente a una velocidad que depende del coeficiente R/L. A su recíproco se le denomina constante de tiempo τ=L/R. Este parámetro es importante ya que establece la frontera entre régimen transitorio y permanente ( t≥5τ).
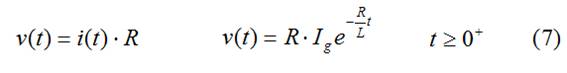
(6) está definida para t≥0 por la condición de continuidad de la I
(7) está definida para t≥0+, en t=0 existe discontinuidad de la V (V(0-)=0, V(0+)= RIg)
3.2 Respuesta natural de un circuito RC
Objetivo: Calcular la evolución de la tensión v(t) en el circuito RC cuando desconectamos la alimentación.
El conmutador ha permanecido mucho tiempo en a.
Condiciones iniciales:
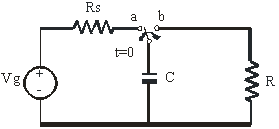
Si pasamos el conmutador de 
el circuito queda:
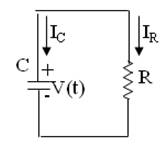
Aplicando KCL:
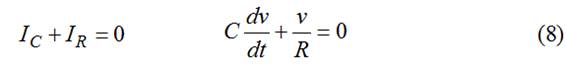
Solución general:
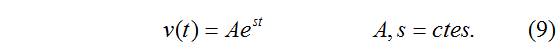
Cálculo de s:
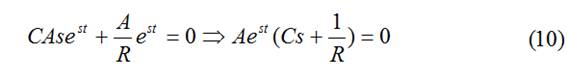
descartando A=0
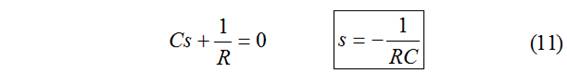
Cálculo de A:
y condiciones iniciales
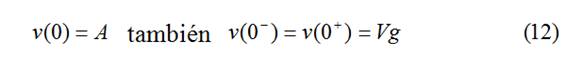
Sustituyendo (12) y (11) en (9)
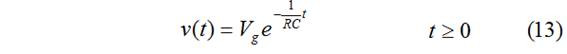
En este caso τ=RC donde R=Requi que "ve" C
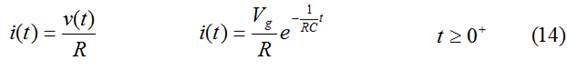
(13) está definida para t≥0 por la condición de continuidad de la V
(14) está definida para t≥0+, en t=0 existe discontinuidad de la I (I(0-)=0, I(0+)= Vg/R)
3.3 Respuesta al escalón de un circuito RL
Objetivo: Calcular la evolución de la corriente i(t) en el circuito RL cuando conectamos una alimentación.
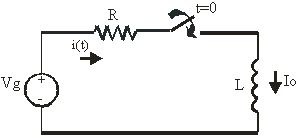
El interruptor ha permanecido abierto mucho tiempo.
Condición inicial 
; L puede tener energía almacenada que se traduce en una corriente inicial no nula (iL(0-) = Io).
En t=0 se cierra el interruptor:
Aplicando KLV:
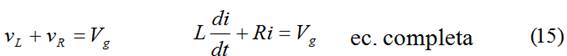
Solución completa = (sol. particular + sol. general):
Sol. particular= valor final de la variable [i(t=∞)]
En t=∞ se alcanza régimen estacionario (c.c.) → L ccto.
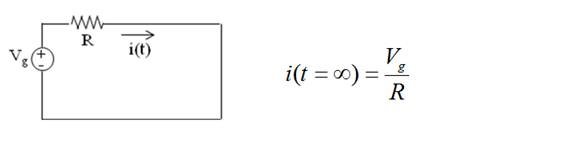
Solución completa = (sol. particular + sol. general):
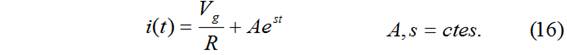
Cálculo de s:
(16)→(15)
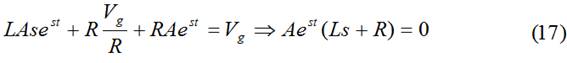
descartando A=0
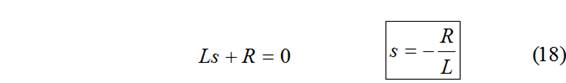
Cálculo de A:
t=0→(16) y condiciones iniciales
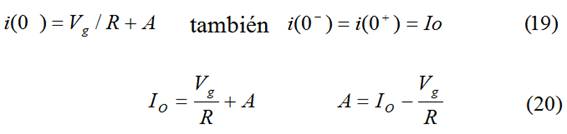
Sustituyendo (18) y (20) en (16)
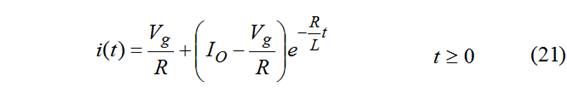
Aplicar ley de Ohm para cálculo de v(t), definida para t≥0+.
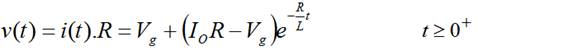
3.4 Respuesta al escalón de un circuito RC
Objetivo: Calcular la evolución de la tensión v(t) en el circuito RC cuando conectamos la alimentación.
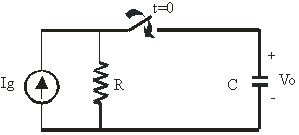
El interruptor ha permanecido mucho tiempo abierto.
Condición inicial 
; C puede tener energía almacenada que se traduce en una tensión inicial no nula (Vc(0-) =Vo).
En t=0 se cierra el interruptor:
Aplicando KCL:
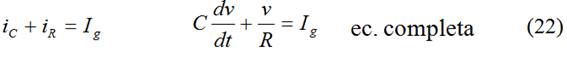
Solución completa = (sol. particular + sol. general):
Sol. particular= valor final de la variable [v(t=∞)]
En t=∞ se alcanza régimen estacionario (c.c.) → C cto. ab.
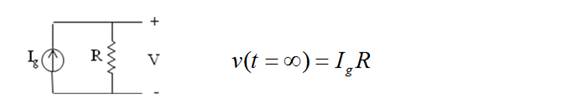
Solución completa = (sol. particular + sol. general):
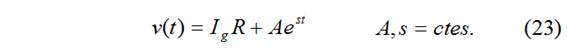
Cálculo de s:
Es la misma que la resp. natural.
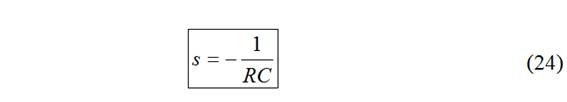
Cálculo de A:
t=0→(23) y condiciones iniciales
Sustituyendo (24) y (25) en (23)
Aplicar ley de Ohm para cálculo de i(t), definida para t≥0+.
3.5 Formula general para circuitos de 1er orden
La solución al circuito RL y RC que engloba la resp. natural y la resp. escalón se puede generalizar:
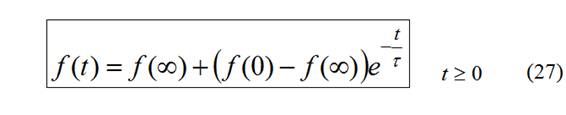
Valor inicial f(0): establecido por las condiciones iniciales del circuito en cuanto a la energía almacenada en L y C.
Resolución de circuitos:
- Dibujar el circuito para
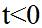y calcular en régimen permanente vC (0-) o iL(0-).
- Aplicar continuidad iL(0-)=iL(0+), vC(0-)=vC(0+).
- Dibujar el circuito para
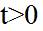y calcular la RTH "vista" por C o L. Calcular τ.
- Calcular para régimen permanente el valor final de iL(∞) o vC(∞).
- Aplicar la fórmula general (27).
Autoevaluación:
- Considera el circuito de la figura que parte de un estado inicial estacionario.
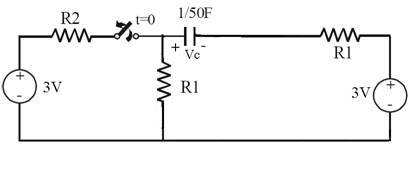
Datos: R1 = 10 Ω y R2 = 20 Ω.
1 |
La tensión en el condensador (Vc) en t=0+ tiene un valor de: |
2 |
La tensión final en el condensador (Vc) cuando se alcanza de nuevo el estado estacionario tiene un valor de: |
3 |
La constante de tiempo (
|
= -1/s) del circuito tiene un valor de:
