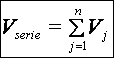Simplificación de circuitos con componentes básicos
Se trata de ir reduciendo un circuito a otro más simple y equivalente. Para ello aplicaremos los lemas de Kirchhoff.
3.1 Asociación de resistencias en serie.
Dos componentes están conectados en serie cuando comparten un nodo al que no llega ningún otro componente del circuito.
Ejemplo:
R1, R2, R3 y Vg están en serie en este circuito
Este circuito es equivalente a este otro:
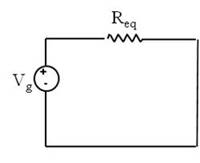
Donde: 
Demostración:
- Aplicamos KCL a los nodos:
(a) 
(b) 
(c) 
(d) 
Por tanto: 
[1]
- Aplicamos KVL a la malla (en sentido horario):
[2]
- Aplicamos la ley de Ohm a cada resistencia:
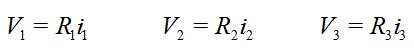[3]
Entonces de [2], aplicando [1] y [3] obtenemos:
de donde deducimos: 
Conclusión: Las resistencias en serie se suman
3.2 Asociación de resistencias en paralelo
Dos componentes están conectados en paralelo cuando los nodos a que se conectan sus terminales coinciden.
La tensión entre los terminales de componentes es la misma (KVL).
Ejemplo: Asociación de resistencias en paralelo.
Conclusión: Las conductancias en paralelo se suman
El caso particular de dos resistencias en paralelo:
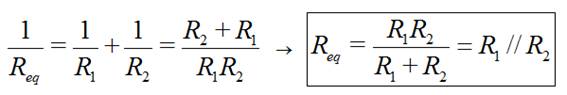
NOTA: Una resistencia en paralelo con un cortocircuito es un cortocircuito.
Autoevaluación:
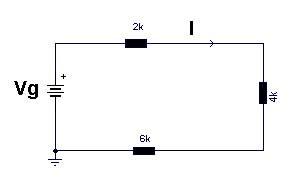
- Considere el circuito de la figura para una alimentación (Vg) de 24 voltios.
1 |
Hallar el valor de la corriente (I) que recorre el circuito. |
2 |
Hallar la caída de tensión en la resistencia de 6 KΩ. |
3 |
Hallar la potencia consumida por la resistencia de 2K. |
.
Ejercicio propuesto de asociación de resistencias en serie y paralelo.
Aplicando asociación de resistencias en serie y paralelo, obtener la resistencia equivalente entre los terminales a, b del siguiente circuito:
3.3 Transformación Δ - Y
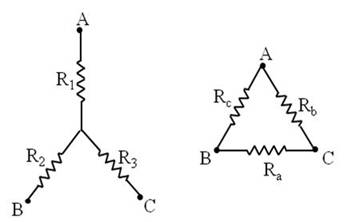
| Configuración Y | Configuración Δ |
 |
 |
 |
 |
 |
 |
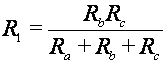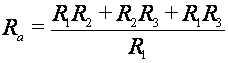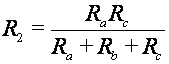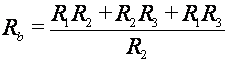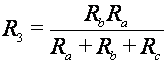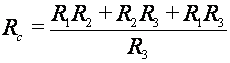Ejercicio propuesto de aplicación de transformación Δ-Y:
Obtener la resistencia equivalente entre los nodos A y B (RAB):
Autoevaluación:
- Dada la siguiente malla de resistencias todas iguales de valor R. (fig. 1)
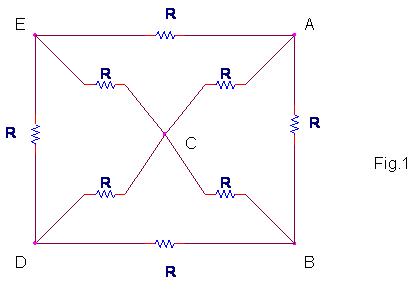
4 |
¿Cual es el valor de la Resistencia equivalente obtenida entre los nodos A y B ? |
5 |
¿Cual es el valor de la resistencia equivalente entre los nodos A y C ? |
6 |
¿Cual es eln valor de la resistencia equivalente entre los nodos A y D? |
.
3.4 Asociación de condensadores en serie
Donde
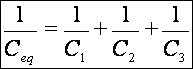
Demostración:
Aplicando KCL al circuito de la izquierda:
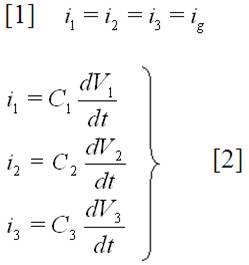
Aplicando KVL en el mismo circuito:
[3] 
En el circuito de la derecha aplicando [3]:
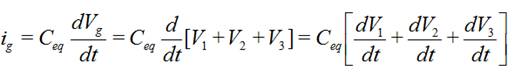
Despejando de [2]:
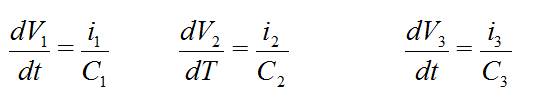
Sustituyendo y utilizando [1]:
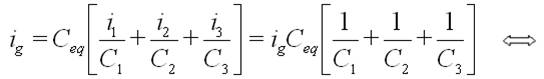
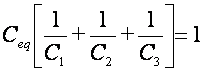
Por tanto:
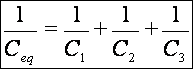
3.5 Asociación de condensadores en paralelo.
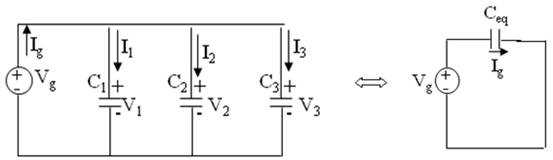
Donde: 
Demostración:
Aplicando KCL al circuito de la izda.:
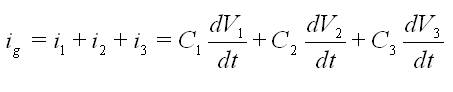
Aplicando KVL:
Por tanto:
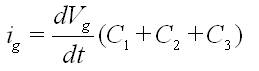
En el circuito de la dcha.:
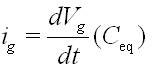
Conclusión: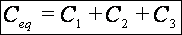 
3.6 Asociación de bobinas en serie/paralelo
La asociación de bobinas sigue la regla de las resistencias:
La demostración es similar al caso de los condensadores.
3.7 Asociación serie/paralelo de fuentes
Fuentes de tensión
- Consideremos la siguiente asociación en serie:
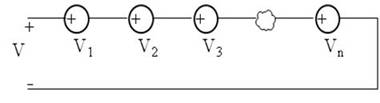
Aplicando KVL :
V = V1 + V2 + V3 + ... Vn
Por tanto:
La corriente no está definida (sólo se define cuando cerramos el circuito)
- Asociación de fuentes en paralelo:
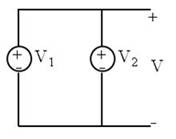
Para fuentes ideales, si 
Aplicando KVL: 
¡Contradicción con el enunciado: 
!
Conclusión: Es imposible conectar dos fuentes ideales de tensión en paralelo con diferente voltaje.
Sin embargo sí podemos conectar dos fuentes reales en paralelo.
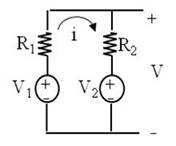
Pero es algo que no debemos hacer en la práctica.
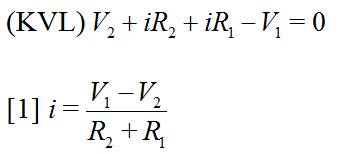
Dado que R1 y R2 son muy pequeñas (Rg→0 en fuentes reales de tensión), para V1 y V2 tal que 
, el resultado de [1] será muy elevado, por lo tanto podemos quemar las fuentes de tensión al conectarlas en paralelo.
Fuentes de corriente
- Asociación en paralelo:
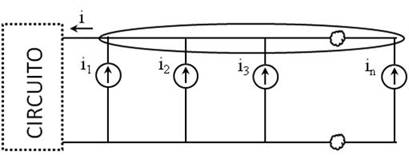
KCL: 
Por tanto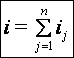 
En una conexión en paralelo de fuentes de corriente, la corriente total es la suma de las corrientes de las fuentes individuales.
La tensión NO está definida a menos que conozcamos el circuito.
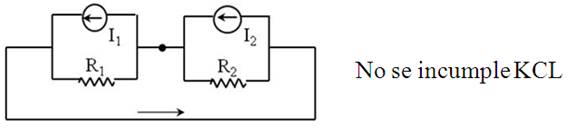
- Asociación de fuentes de corriente en serie:
Asociación de fuentes de corriente ideales distintas en serie:
Fuentes ideales 
Se llega a una paradoja, ya que según KCL, las corrientes que entran en un nodo son iguales a las que salen, por lo que 
Sin embargo SI podemos conectar dos fuentes de corriente reales en serie.
3.8 Movilidad de fuentes
Fuentes de tensión:
Supongamos una fuente de tensión V conectada a 3 componentes electrónicos (R, L, o C):
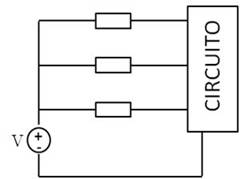
Si se sustituye por 3 fuentes en paralelo y se conecta cada una a una rama, el circuito sería equivalente:
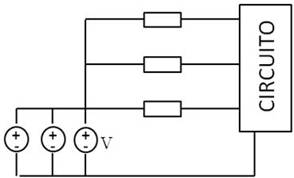
También es equivalente esta representación:
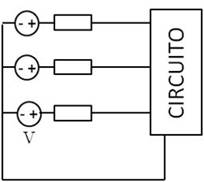
De igual forma, también existe movilidad a la derecha:
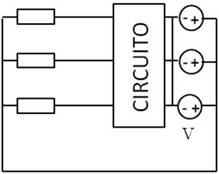
Fuentes de corriente:
Supongamos ahora una fuente de corriente conectada a una serie de varios componentes electrónicos:
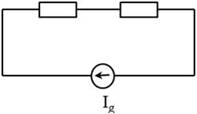
Podemos añadir tantas fuentes en serie como queramos obteniendo el siguiente circuito equivalente:
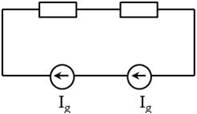
Añadimos un nuevo cable de conexión sin modificar el circuito:
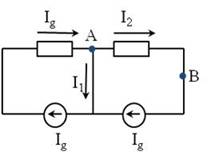
Aplicando KCL en el nodo A:
;
Y aplicando KCL en el nodo B:
;
Por tanto: 
Y el circuito es equivalente a los anteriores.
Entonces podemos también representarlo así:
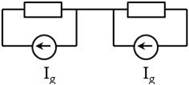
3.9 Transformación de fuentes.
Permite sustituir una fuente de tensión real por una fuente de corriente real:
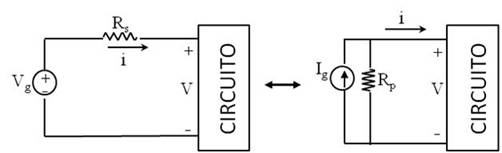
Veamos qué condiciones se deben cumplir para que ambos circuitos sean equivalentes:
i,V deben ser los mismos
Para que las dos corrientes sean iguales se debe cumplir que:
Conclusión:
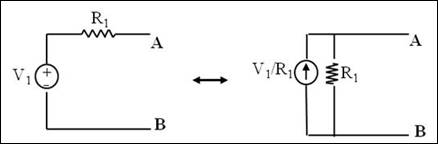
¡IMPORTANTE!
Conservar el sentido de la corriente con relación a la polaridad de la fuente de tensión.
